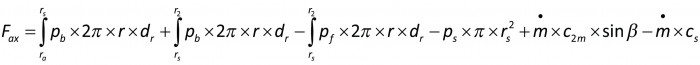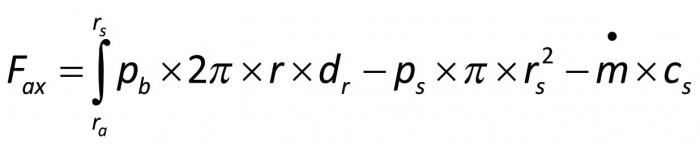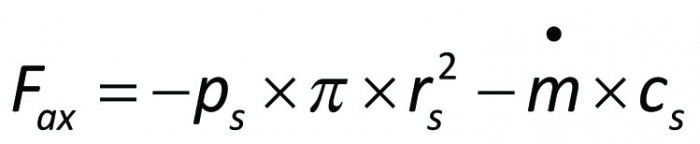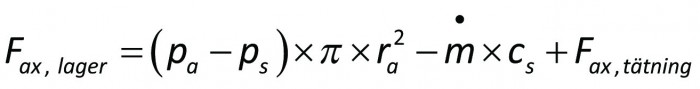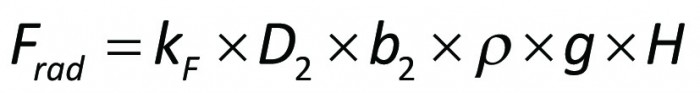Pumpars axialkrafter och radialkrafter

Den resulterande axialkraften på pumpaxeln måste tas upp av lagringen eller balanseras ut med en särskild anordning. En särskild balanseringsskiva kräver emellertid alltid en viss driveffekt och nedsätter därmed pumpens totalverkningsgrad. Det är därför fördelaktigt om axialkraften kan begränsas direkt genom pumphjulets utformning.

Figur 3.11 Illustration till axialkrafter

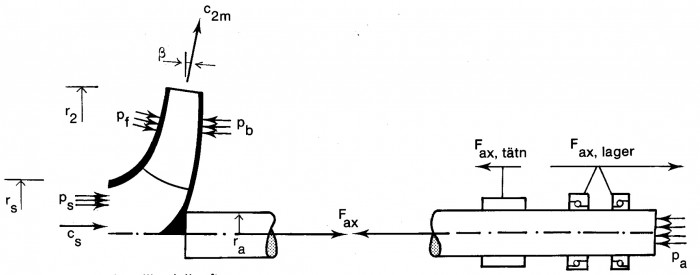
Genom att tillämpa impulsekvationen – ekv. 11.7 – på en kontrollvolym, som just precis omsluter pumphjulet, erhålles med beteckningar enligt figur 3.11.

Ekv 3.18 a

Om trycken på pumphjulets fram- och baksidor för r > r_s antages vara lika, (p_b=p_f) och om vinkeln β är liten, (sin β ~ 0) förenklas uttrycket ovan till

Ekv 3.18 b

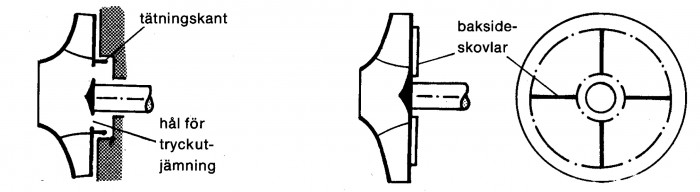
En vanlig åtgärd i avsikt att begränsa F_ax är att förse pumphjulets baksida med en extra tätningskant och att samtidigt borra upp hål för tryckutjämning. Då blir

Ekv 3.18 c

Utöver axialkraften från pumphjulet verkar på axeln även krafter från tätningar och lager samt atmosfärstrycket i axeländan. Lagerkraften blir

Ekv 3.18 d

Vid höga systemtryck (p_s stort) kan axialkraften trots extra tätningskant och tryckutjämningshål anta avsevärda belopp.

Figur 3.12 Metoder för begränsning av axialkraften

Ett annat sätt att begränsa axialkraften är att förse pumphjulet med baksideskovlar. Därigenom ges vätskan en kraftigare medrotation på baksidan än vad friktionen åstadkommer på framsidan. Den ökade medrotationen medför lägre tryck för r < r2 och därmed även en reducering av axialkraften.

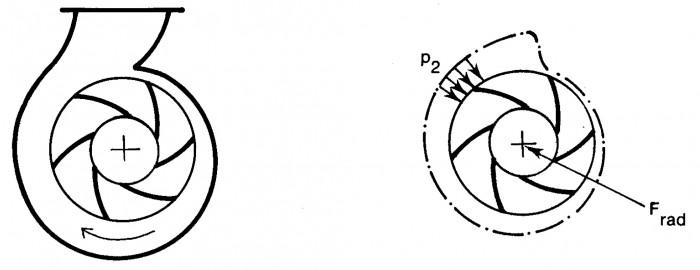
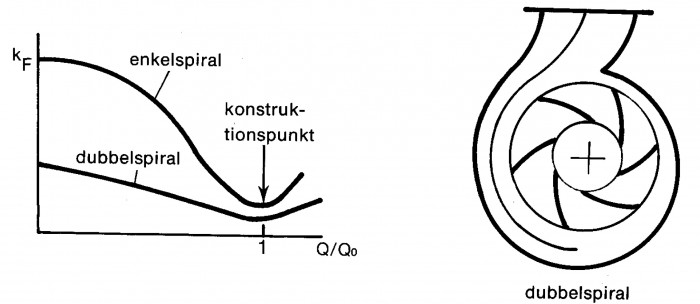
Vid flerstegspumpar eller vid dubbelsidigt sugande pumphjul erhålles små axialkrafter genom motriktad placering av hjulinloppen. I alla pumpar utrustade med spiralhus uppträder vid dellast avsevärda radialkrafter.

I konstruktionspunkten eftersträvas en jämn tryckfördelning runt pumphjulet. Detta villkor bestämmer spiralhusets form. Vid dellast kommer emellertid trycket att variera längs hjulets periferi. Den radiella kraften på pumphjulet tas upp av lagringen via axeln.

Figur 3.13 a Illustration till radialkraft på pumphjulet vid reducerat flöde (Q<Q0)

Eftersom trycket varierar längs hjulets periferi, kommer även strömningen i de olika skovelluckorna att variera då pumphjulet roterar.

Ekv 3.19

där

F_rad = radiell kraft (N)

k_F = dimensionslös parameter

D₂ = hjulets ytterdiameter (m)

b₂ = hjulets utloppsbredd (m)

ρ = vätskans densitet (kg/m³)

g = jordaccelerationen 9,806 (m/s²)

H = uppfordringshöjd (m)

Parametern k_F antar olika värden för olika pumputföranden och varierar dessutom kraftigt med volymflödet genom pumpen.

Figur 3.13b: Exempel på inverkan av driftspunktens läge och spiralhusets utformning på parametern k.

För en centrifugalpump med enkelspiral kan kF anta värden upp till 0,4 i dämda punkten (Q=0).

Ett effektivt sätt att begränsa radialkraftens storlek är att förse spiralhuset med en extra mellanvägg.

Radialkraften är som störst vid Q=0 (dämda punkten). Radialkraften orsakar en utböjning av pumpaxeln och utsätter axeln för roterande utmattning. Som riktvärde för axelns dimensionering används ofta villkoret att axelns utböjning vid dämda punkten skall vara mindre 0,05 mm vid axeltätningen.

Axial- och radialkraftens storlek är av avgörande betydelse för pumpens konstruktiva uppbyggnad (dimensionering av spel, lagring etc). De är även ofta primärorsaken till haverier. Observera att både axial- och radialkraften ökar vid dellast och är som störst vid dämda punkten.