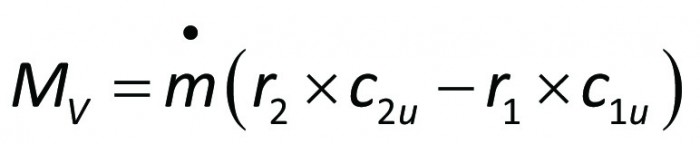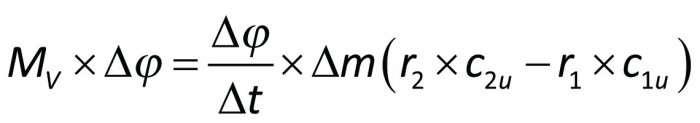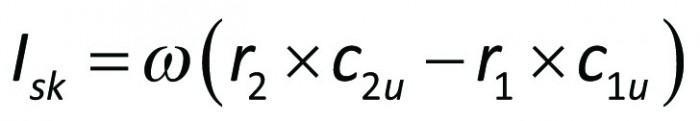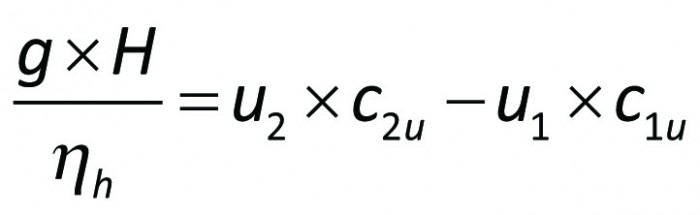Eulers ekvation

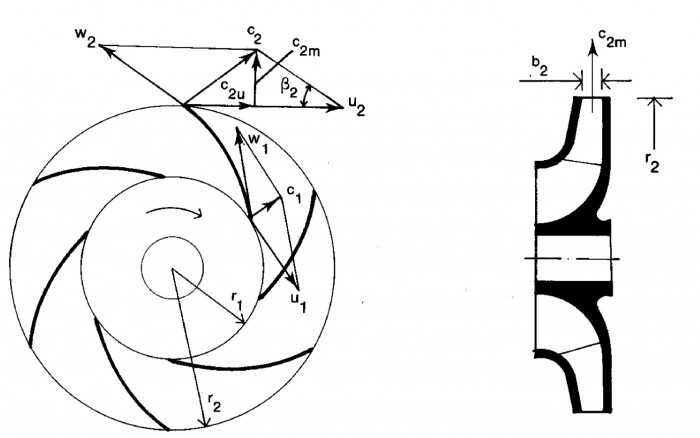
Figur 3.7 visar ett pumphjul med tillhörande hastighetstrianglar. Pumphjulet anströmmas av vätskan med hastigheten c₁ vid radien r₁. Vätskan lämnar pumphjulet vid radien r₂ med hastigheten c₂. Genom skovelns utformning tvingas den relativa hastigheten – dvs den hastighet, som upplevs av en observatör, som medföljer skoveln i dess rörelse – att ändra storlek och riktning från w₁ till w₂. Därigenom kommer även absoluthastigheten c₂ vid hjulutloppet att avvika från anströmningshastigheten c₁. Absoluthastighetens komponent i tangentiell led, dvs i periferihastighetens riktning betecknas c_u.

Figur 3.7 Pumphjul med hastighetstrianglar vid inlopp och utlopp

Genom att tillämpa den från strömningsläran kända impulsmomentlagen på strömningen genom pumphjulet erhålles i tangentiell led

Ekv 3.8

Här är M_v det vridande moment, med pumphjulet måste påverka vätskan, för att strömningen enligt figur 3.7 skall kunna existera. Strömningshastigheterna i ekvation 3.8 avser att vara representativa medelvärden för det medium, som genomströmmar pumphjulet. Under tiden Δt vrider sig pumpaxeln vinkeln Δφ samtidigt som massan Δm passerar in och en lika stor massa Δm passerar ut genom pumphjulet. Multipliceras båda leden med Δφ och samtidigt m = Δm/Δt införes, blir

Ekv 3.9

Men M_v · Δφ/Δm är det arbete per massenhet, som det vridande momentet utför under det att pumphjulet vrider sig vinkeln Δφ. Detta arbete per massenhet kallas skovelarbete och betecknas I_sk. Vidare är kvoten Δφ/Δt lika med pumphjulets konstanta vinkelhastighet ω. Därigenom blir

Ekv 3.10

Av skovelarbetet resulterar den del, som motsvarar skovelförlusterna i en ökning av mediets inre energi, medan resten ( h · I_sk) ger en nyttig tillståndsförändring hos vätskan (g · H). Införes vidare periferihastigheten u = r · ω erhålles slutligen

Ekv 3.11

Ekvation 3.11 är Eulers ekvation så som den vanligen skrivs för pumpar, där:

g = jordaccelerationen 9,806 (m/s²)

H = uppfordringshöjd (m)

η_h = hydraulisk verkningsgrad

u = periferihastighet (m/s)

c_u = absoluthastighetens tangentialkomponent (m/s)