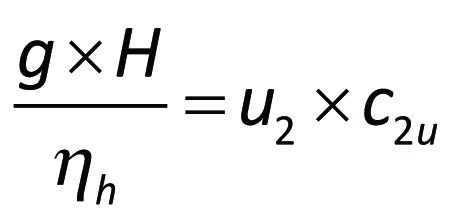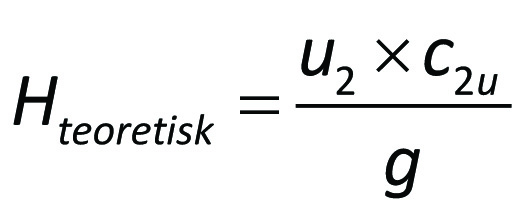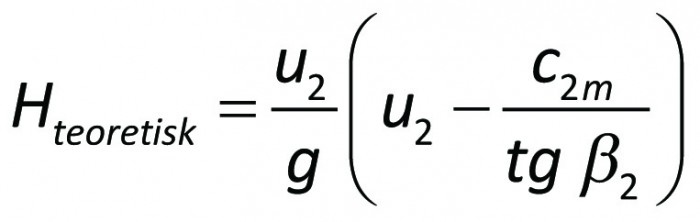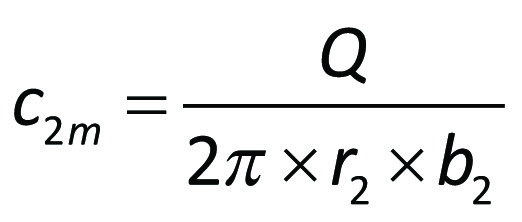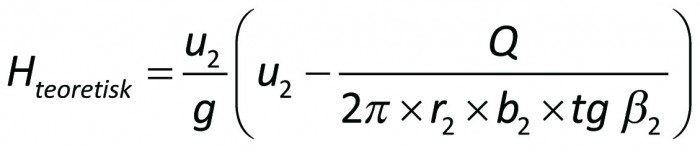- 1 Installation av pumpar
- 2 Skötsel och Underhåll av pumpar
- 3 Pumpar, funktion och konstruktion
- 3.1 Allmänt om Pumptyper
- 3.2 Rotordynamiska pumpars grunder
- 3.3 Förträngningspumpars grunder
- 3.4 Pumpkurvor
- 3.5 Pumpars sugförmåga, NPSH och kavitation
- 3.6 Centrifugalpumpars utföranden
- 3.6.1 Vattenpumpar
- 3.6.2 VVS pumpar
- 3.6.3 Vattenautomater
- 3.6.4 Länspumpar
- 3.6.5 Flerstegspumpar
- 3.6.6 Djupbrunnspumpar
- 3.6.8 Spolpumpar
- 3.6.9 Standardpumpar enligt ISO
- 3.6.10 Kemipumpar och processpumpar
- 3.6.11 Tätningslösa pumpar
- 3.6.12 Pumpar av plast
- 3.6.13 Massapumpar
- 3.6.14 Godspumpar
- 3.6.15 Livsmedelspumpar
- 3.6.16 Stockningsfria pumpar
- 3.6.17 Dubbelsidigt sugande pumpar
- 3.6.18 Propellerpumpar
- 3.7 Vätskeringpumpar
- 3.8 Förträngningspumpars utförande
- 3.9 Övriga pumpar
- 3.11 Pumpval
- 4 Material och materialval
- 4.1 Inledning
- 4.2 Materialöversikt för pumpar
- 4.3 Materialhållfasthet och trycktäthet för pumpar
- 4.4 Korrosion och Erosion på pumpar
- 4.5 Materialval pumpar för slitande vätskor
- 4.6 Kavitationsbeständiga material i pumpar
- 4.7 Materialkombinationer och materialval i pumpar
- 4.8 Praktiska problemställningar vid materialval för pumpar
- 5 Pumptätningar
- 6 Axelkopplingar för pumpar
- 6.2 Val av axelkoppling
- 6.3 Typ av koppling för pumpar
- 6.4 Uppriktningsfel för pumpar
- 6.5 Axelkopplingar, krafter och moment
- 6.6 Pumpkopplingar och dess driftsfaktorer
- 6.7 Pumpkopplingars varvtal, dimensioner och vikt
- 6.10 Pumpkopplingar, uppställning och demontering
- 6.11 Pumpkopplingars livslängd och kostnader
- 6.12 Pumpaxlars uppriktning
- 7 Drivutrustning för pumpar
- 8 Flödesreglering för pumpar
- 8.2 Anpassning av pumphjulets diameter
- 8.3 Seriekoppling och parallellkoppling av pumpar
- 8.4 Polomkopplingsbar asynkronmotor
- 8.5 Start och stoppreglering av pumpar
- 8.6 Driftsföljder vid start- stoppreglering
- 8.7 Magasinsvolymer vid start-stopp reglering
- 8.8 Kontinuerlig reglering av pumpar
- 8.9 Strypreglering av pumpar
- 8.10 Shuntreglering av pumpar
- 8.11 Varvtalsreglering av pumpar
- 8.12 Ekonomiska aspekter vid varvtalsreglering av pumpar
- 8.13 Val av utrustning för varvtalsreglering av pumpar
- 9 Storheter och enheter för pumpar
- 10 Vätskors egenskaper
- 11 Vätskeströmning
-
Den teoretiska pumpkurvan
Den teoretiska pumpkurvan beskrivs som pumpkurvan utan förluster. Om strömningen vore förlustfri kan den teoretiska uppfordringshöjden beräknas.
(För mer information om olika pumpars pumpkurvor se kapitel 3.4 Pumpkurvor för olika pumptyper.)
Enligt Eulers ekvation är pumpens uppfordringshöjd beroende av hastighetstrianglarnas utseende och av de hydrauliska förlusternas storlek. Båda dessa faktorer påverkas bl.a. av den volymström Q som passerar genom pumpen.
I många fall är absoluthastighetens tangentialkomponent framför pumphjulet liten, dvs c1u ≅ 0. Då förenklas Eulers ekvation till
Om strömningen genom pumpen vore förlustfri ηh = 1), skulle den teoretiska uppfordringshöjden
erhållas. Med ledning av figur 3.7 blir
och
eller
Vinkeln β2, som är markerad i hastighetstriangeln, är något mindre än skovelvinkeln i hjulutloppet. Denna vinkelskillnad kallas deviationsvinkel och beror på skovlarnas bristande förmåga att helt styra relativströmningen. Deviationsvinkelns storlek är i första hand beroende av skovelantalet.
-
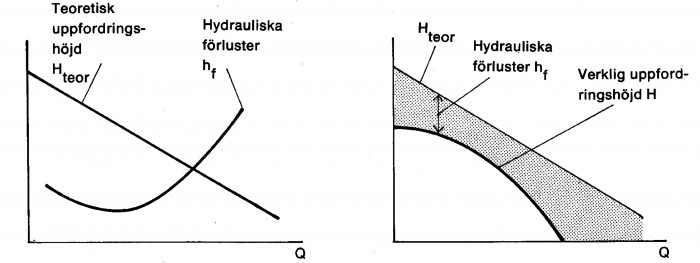
För en given pump, som arbetar med ett visst konstant varvtal, avtar enligt ekvation 3.14 den teoretiska uppfordringshöjden Hteor linjärt med ökande volymström Q.
Den verkliga uppfrodringshöjden H skiljer sig från Hteor genom de hydrauliska förlusterna hf. Dessa är som vid alla andra strömningsfall beroende av anströmningsriktningen mot den omströmmade kroppen. Vid pumpar varierar anströmningsriktningen mot exempelvis skovlarna med volymströmmen. Vid en viss anströmningsvinkel erhålles den gynnsammaste strömningen och därmed de minsta förlusterna. Vid såväl högre som lägre värden på Q ökar hf. Genom att subtrahera hf från Hteor erhålles pumpens verkliga QHkurva vid konstant varvtal – figur 3.8. Beroende på olika värden på de parametrar, som ingår i Hteor och hf, dvs olika konstruktiva utformningar, varierar QH-kurvans form från pumptyp till pumptyp.
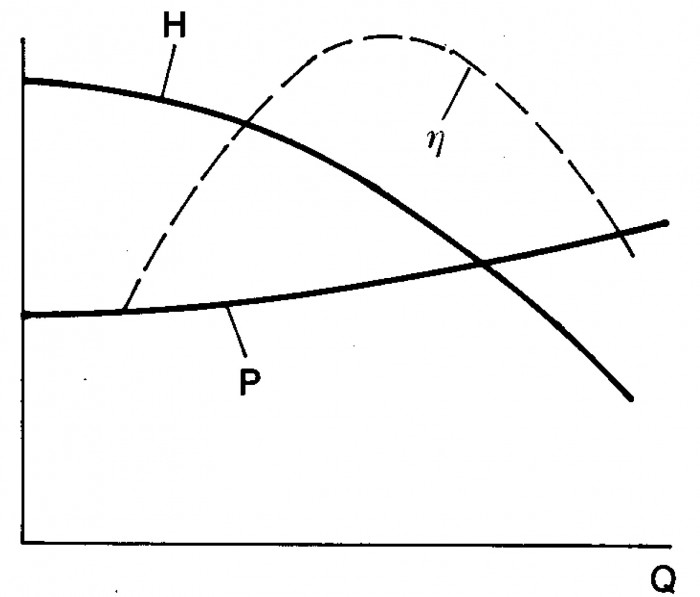
Utöver pumpens QH kurva brukar även som i figur 3.9, erforderlig axeleffekt P och pumpens verkningsgrad η anges som funktion av volymströmen i ett pumpdiagram. Pumpen kan i princip arbeta i vilken punkt som helst längs QH kurvan. Driftpunktens läge i ett verkligt fall bestäms av egenskaperna hos det system som pumpen är inkopplad i.