Vätskeströmning

Inledning, några begrepp och förutsättningar

De strömningsförlopp, som förekommer i naturen, är oftast mycket komplicerade och svårbehandlade. I många tekniska sammanhang kan man dock erhålla fullt godtagbara resultat från beräkningar baserade på förenklade betraktelsesätt. Nedan diskuteras några av de begrepp och förutsättningar, som är aktuella i detta sammanhang.

Ett strömningsförlopp är stationärt om alla strömningsparametrar – tryck, hastighet, etc i en viss bestämd punkt i strömningsfältet är oberoende av tiden. Enligt denna definition är så gott som samtliga förekommande strömningsförlopp instationära. Många förlopp kan dock behandlas som stationära (t ex turbulent strömning) utan att noggrannheten äventyras. Detta sker genom att tidsmedelvärden införes på lämpligt sätt. De i senare avsnitt presenterade grundekvationerna gäller för stationär strömning.

l allmänhet är strömningar tredimensionella dvs strömningsparametrarna varierar med alla de tre koordinater, som erfordras för att definiera en punkt i rymden. Vid många tekniskt viktiga strömningsfall kan man med bibehållen noggrannhet reducera antalet studerade dimensioner. Ett sådant exempel är rörströmning där strömningsparametrarna antages variera enbart i en dimension nämligen rörets längdriktning. Endimensionell strömning förutsätter att strömningsparametrarna beskrives med hjälp av medelvärden över strömningstvärsnitten. I princip borde olika medelvärden bildas då kontinuitet, impuls och energi studeras. Vid rörströmning definieras strömningens medelhastighet i röret som volymströmmen dividerad med rörets tvärsnittarea (c = O/A)*. Denna medelhastighet kan som regel med tillräcklig noggrannhet användas i de flesta sammanhang.

En viktig egenskap hos ett strömmande medium är dess densitet och de förändringar som densiteten undergår vid strömningen. En gas pressas samman – densiteten ökar – då trycket någonstans i strömningsfältet stiger. En sådan strömning kallas kompressibel. l en vätska ändrar sig densiteten mycket litet även vid stora tryckändringar. Vätskeströmning kan därför oftast med god noggrannhet behandlas som inkompressibel. Detta gäller även gasströmning vid låga hastigheter, då tryckändringarna är obetydliga.

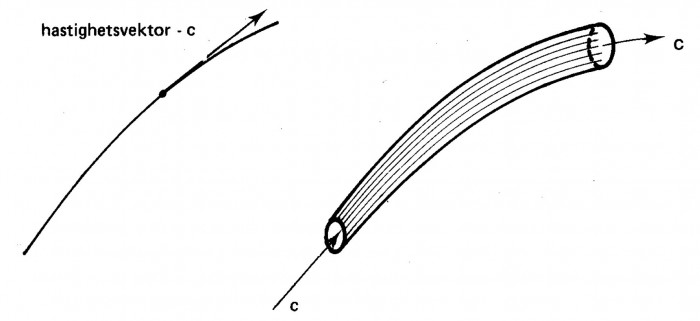
En strömlinje är en kurva till vilken hastighetsvektorn är tangent i varje punkt. Vid stationär strömning förblir strömlinjerna oförändrade i tiden och representerar då även den väg en vätskepartikel tar genom strömningsfältet. Strömlinjerna genom alla punkter på en sluten kurva i strömningsfältet bildar ett strömrör. Genom strömrörets begränsningsyta kommer ingen massa att passera. Strömröret påminner därigenom om ett vanligt rör. Vid ett vanligt rör förekommer emellertid alltid starka friktionseffekter vid rörväggen vilket inte är nödvändigt vid ett strömrör.

Figur 11.1 Strömlinje och strömrör

*Strömningshastigheten betecknas omväxlande med c eller v.