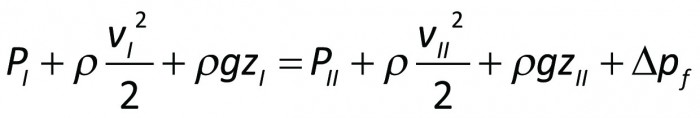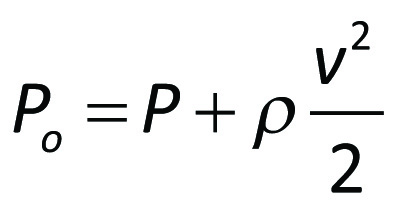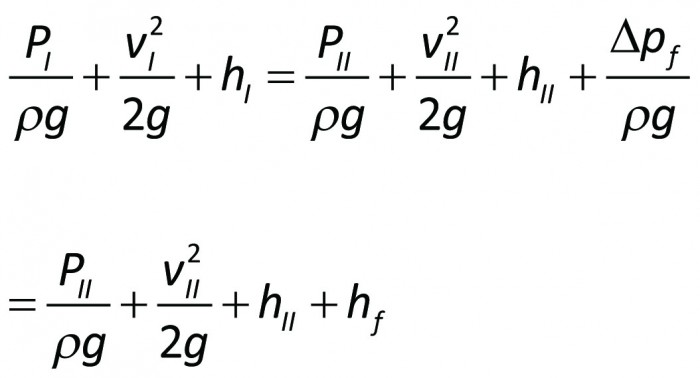11.1.2 Bernoullis ekvation

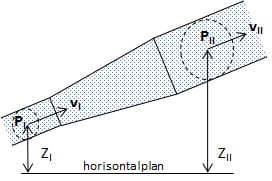
Bernoullis ekvation är en rörelseekvation, dvs den är en omformulering av utgångssambandet ”kraften = massan x accelerationen”. Bernoullis ekvation gäller därför oberoende av om värme tillföres eller ej under förloppet. Bernoullis ekvation för den stationära, endimensionella och inkompressibla strömningen mellan läge I och II lyder

Ekv 11.4

där

p = statiskt tryck [N/m² eller Pa]
ρ= vätskans densitet [kg/m³]
v = strömningshastighet [m/s]
g = jordaccelerationen 9,806 [m/s²]
z = höjd över ett utvalt horisontalplan [m]
Δpf = strömningsförluster [N/m² eller Pa]

Figur 11.4 Beteckningar till Bernoullis ekvation

Termen ρv²/2 kallas för dynamiskt tryck och slås ibland samman med det statiska trycket P till totaltrycket P_o.

Ekv 11.5

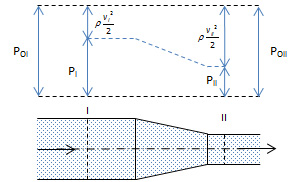
Vid en förlustfri ( pf=0) och horisontell (h_I=h_II) strömning förändras ej totaltrycket. Om det dynamiska trycket (hastigheten) ökar kommer det statiska trycket att minska i motsvarande grad. Hastigheten i ett rör ökar då arean (diametern) minskar.

Figur 11.5 Förlustfri, horisontell rörströmning

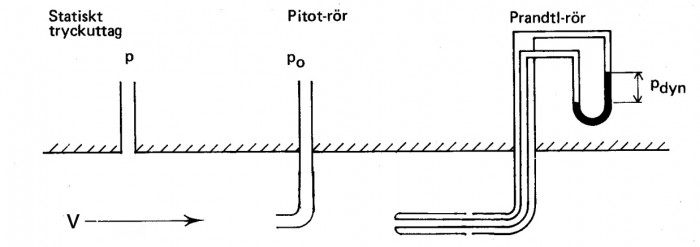
Totalt och statiskt tryck

Totalt och statiskt tryck mätes på olika sätt.

• Ett tryckuttag, som är vinkelrätt mot strömningsriktningen, känner av det statiska trycket.
• Framför ett pitot-rör bromsas hastigheten upp och statiska trycket stiger. Vid pitot-rörets mynning är hastigheten lika med noll. Pitot-röret känner därför av totaltrycket i strömningen.

Totaltrycket är som regel enkelt att mäta medan det statiska trycket lättare blir behäftat med mätfel.

• Med ett Prandtl-rör mätes både totalt och statiskt tryck. Kopplas dessa mot varandra erhålles direkt det dynamiska trycket ρv²/2.

Figur 11.6 Mätning av statiskt, totalt och dynamiskt tryck.

Av de återstående termerna i Bernoullis ekvation motsvarar ρ · g · h det statiska tryck, som en vätskepelare med höjden h (enligt z i figur 11.4)  skapar.

Termen p_f utgör det tryckfall, som förorsakas av friktionsbetingade strömningsförluster. Inom pumptekniken är det ofta praktiskt att använda sig av uttrycksformen meter vätskepelare [m vp].

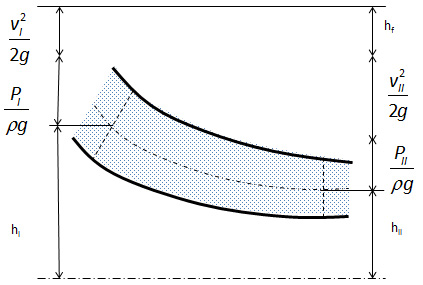
Om alla termer i Bernoullis ekvation divideras med g erhålles

Ekv 11.6

De olika termerna kallas då

Eftersom alla termer i ekvation (11.6) har karaktären av en höjd, kan de lätt åskådliggöras grafiskt.

Figur 11.7 Grafisk illustration av Bernoullis ekvation.