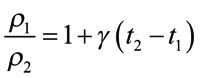Vätskors densitet och volymutvidgning

Vätskors densitet

Enhet kg/m³. Beteckning ρ (rå).

Densitet är förhållandet mellan en materialmängds massa och volym. Uppgifter om densitet erfordras för beräkning av tryck och pumpens effektbehov.

Vätskors densitet vid 25°C anges i vätsketabellerna i avsnitt 10.9. Densiteten förändras under inverkan av:

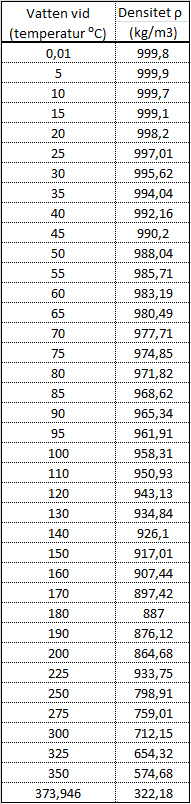
• Temperatur se tabell 10.10
• Koncentration och blandningsförhållande, se figur 10.18-10.21.
• Halt av och storlek på fasta partiklar i suspensioner, se avsnitt 10.7 och 10.8

Andra egenskaper som en vätskas förmåga att lösa luft, gas, är beroende av temperatur och tryck och påverkar densiteten endast obetydligt.

Vattens densitet är störst vid 4°C = 1000 kg/m³ då vatten har sin minsta volym. Vatten intar härigenom en särställning bland vätskor. Vid avkylning under 4°C utvidgar sig vattnet ända till 0°C och fryser till is, varvid volymen ökar med 9 %. Isens densitet är då 917 kg/m³.

Densitet för vatten vid olika temperaturer

Vatten har ett densitetsmaximum även när det innehåller lösta salter, men den största densiteten uppträder då under 4°C ju högre salthalten är desto lägre temperatur för max värdet. Havsvatten har sin största densitet något under 0°C, fryspunkten är ännu lägre.

Vätskors volymutvidgning

Enhet ⁰Cˉ¹. Beteckning γ.

Densiteten är temperaturberoende och minskar vid stigande temperatur samt ökar vid fallande. Detta sammanhänger med att vätskans volym ökar vid uppvärmning respektive minskar vid avkylning. Volymändringen hos en vätska kan i princip bestämmas med hjälp av dess volymutvidgningskoefficient γ [⁰Cˉ¹]. Denna är ett uttryck på den volymförändring som sker för varje grads temperaturförändring av vätskan.

Sambandet mellan densiteter ρ1, och ρ2 vid två temperaturer t1, respektive t2 och volymutvidningskoefficienten är:

Ekv. 10.4

Uppgifter om volymutvidgningskoefficienten erfordras för beräkning av tryckändringar hos innestängda vätskevolymer, max- och minimivolymers i öppna och slutna behållare samt vid volymkorrigeringar.

För vatten bör observeras att γ är kraftigt temperaturberoende, varför vid praktiska beräkningar volymändringar bör beräknas med utgångspunkt från densitet vid olika temperaturer. Volymutvidningskoefficienten kommer, då närmast till användning vid interpolering.