Systemkurvor

Systemkurvor

Systemkurvor beskriver pumpsystems motstånd i förhållande till vätskeflöde. Motståndet är friktionsmotstånd i rörledningar vilket varierar beroende på flödet och därför kallas dynamiskt. Dessutom beskriver systemkurvor den geodetisk uppfordringshöjden ofta kallad lyfthöjd eller statisk uppfordringshöjd samt i förekommande fall, skillnaden i tryck mellan tankar där trycket i någon av matningstankar eller mottagande tank avviker ifrån atmosfäriskt tryck.

Pumpens driftspunkt

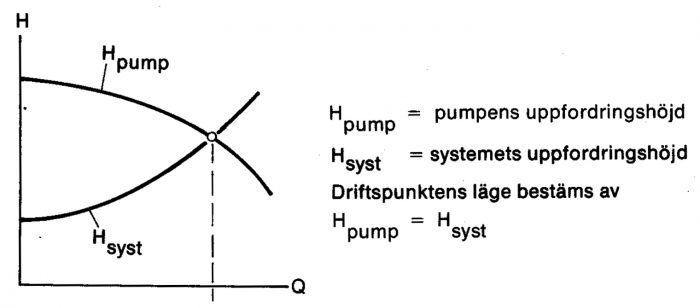
Inkopplad i ett rörsystem kommer pumpen att arbeta i en punkt där jämvikt råder mellan pump och rörsystem. I jämviktsläget är pumpens pådrivande funktion lika stark som systemets bromsande. Pumpens egenskaper i detta avseende redovisas vanligen med hjälp av dess 0-H-kurva. Motsvarande kurva för rörsystemet kallas systemkurva och betecknas Hsyst.

Den volymström, vid vilken pumpkurvan och systemkurvan skär varandra, kommer att passera genom rörsystemet. För att rätt kunna dimensionera pump och rörsystem krävs därför kännedom om dessa båda kurvors egenskaper. Detta avsnitt ägnas åt rörsystemets egenskaper.

Enkla rörsystem

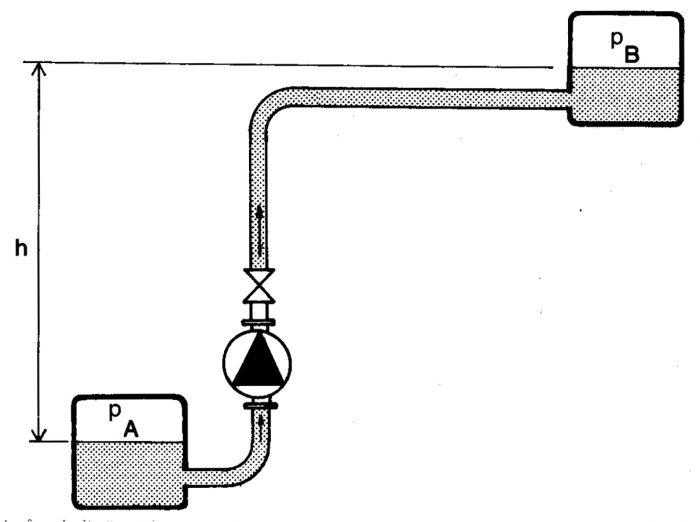
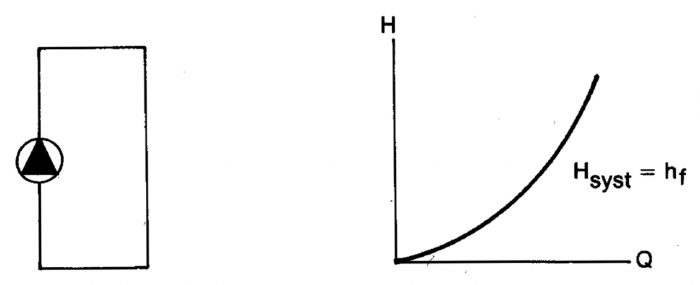
Figur 11.14 Exempel på enkelt rörsystem.

Systemets uppfordringshöjd uppdelas vanligen i en statisk del Hstat och en förlustdel hf.

Hsyst = Hstat + Hf Ekv 11.23

Till den statiska delen, som förutsättes vara oberoende av volymströmmen, räknas skillnad i statiskt tryck och i nivå mellan systemets ränder. Med beteckningar enligt figur 3.14 blir

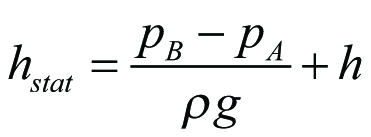
Ekv 11.24

där P = statiskt tryck [N/M]
ρ= vätskans densitet [kg/m3]
g = jordaccelerationen 9,806 [m/s2]
h = nivåskillnad [m]

Till förlustdelen räknas strömningsförluster i rakrör och s k engångsförluster, dvs förluster i böjar, ventiler etc.

Hf = hfr + hfe (Ekv 11.25)

Med gängse beteckningar blir

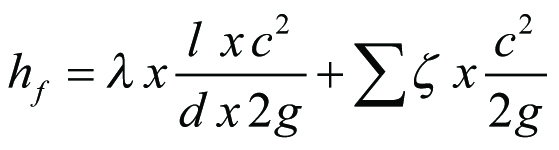
Ekv 11.26

där

λ = förlustkoefficient för rakrör
ζ = förlustkoefficient för böj, ventil etc
Σ ζ = summan av alla förlustkoefficienter
l = rörlängd [m]
d = rördiameter [m]
Q = volymström [m3/s]
c = strömningshastighet [m/s]

För ett givet rörsystem (l,d) är ofta (stora Re) förlustkoeffecienterna λ och ζ oberoende av Q. Man kan då skriva förlusthöjden

hf = konstant – Q 2 Ekv 11.27

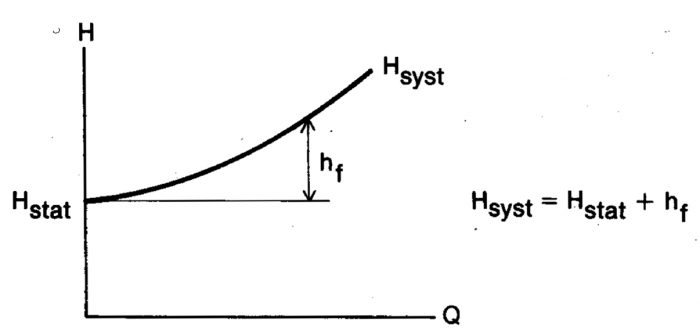
Ofta råder samma tryck pA = pB = atmosfärstryck vid systemets ränder. Därigenom kommer Hstat att bli lika med nivåskillnaden och systemets uppfordringshöjd blir Hsyst Hstat + hf = h + konst · Q2 Ekv 11.28 eller i grafisk form

Figur 11.15 Systemkurva

Observera att det sätt som systemkurvan återgivits på i figur 3.15 förutsätter att pA , pB och h är oberoende av volymströmmen Q. Vidare förutsätts att även λ och ζ är oberoende av Q (Re). Dessa förutsättningar är oftast men ej alltid uppfyllda.

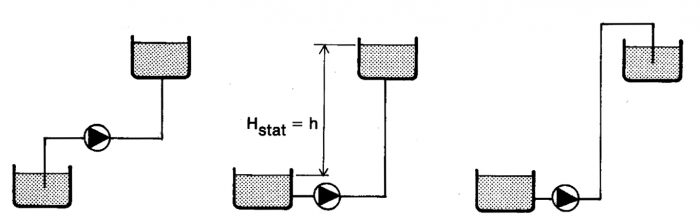
Figur 11.16 visar tre olika rörsystem med samma nivåskillnad och därmed lika statisk uppfordringshöjd.

 

Figur 11.16 Rörsystem med lika statisk uppfordringshöjd.

För vissa rörsystem, t ex för cirkulationssystem, är Hstat = 0 och systemets uppfordringshöjd består enbart av rörströmningsförluster.

Figur 11.17 Rörsystem med Hstat = 0

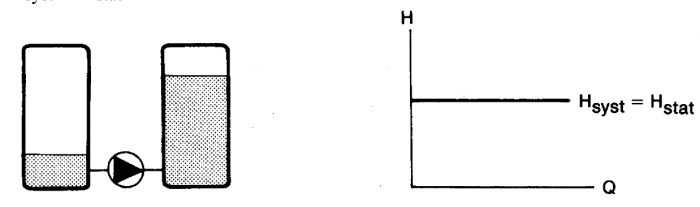
I andra rörsystem med korta ledningar och avsevärda tryck- eller nivåskillnader är strömningsförlusterna försumbara och Hsyst = Hstat.

Figur 11.18 Rörsystem med hf = 0

Systemkurvor i förgrenade rörsystem

Det första exemplet på ett förgrenat rörsystem är ett cirkulationssystem. Vid ett sådant är Hstat = 0. Den volymström Qp, som passerar genom pumpen, delar sig i förgreningspunkten. Av kontinuitetsskäl gäller QP=QA+ QB Ekv 11.29

De båda grenarna A och B har var sin systemkurva, som adderar sig till en resulterande kurva. Skärningspunkten mellan den resulterande systemkurvan och pumpkurvan bestämmer pumpens driftspunkt.

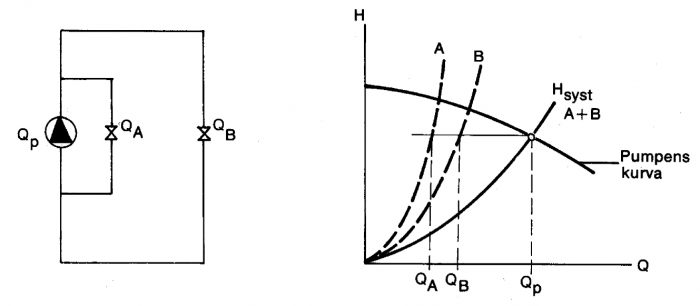
Figur 11.19 Förgrenat cirkulationssystem.

Av figur 11.19 framgår även hur stor del av pumpflödet, som strömmar genom de olika grenarna. Flödets fördelning beror på förlusternas storlek i respektive gren. I detta exempel antages förgreningspunkterna ligga nära pumpen, dvs strömningsförlusterna mellan pump och förgreningspunkter har försummats.

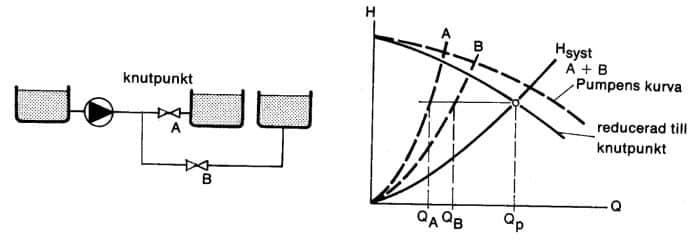
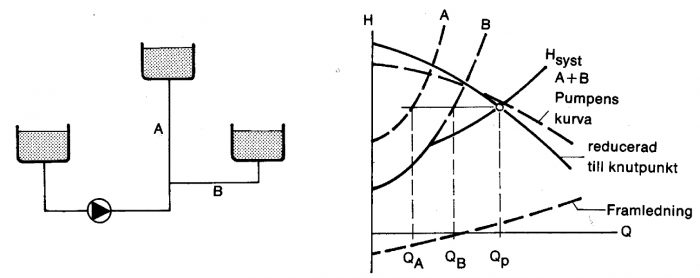
Figur 11.20 Förgrenat rörsystem, Hstat = 0

I nästa exempel, figur 11.20, tas hänsyn även till förlusterna i huvudledningen fram till förgreningspunkten. Detta sker genom att pumpkurvan reduceras med förlusterna fram till knutpunkten. Den reducerade kurvan matchas därefter mot det återstående rörsystemet som förut.

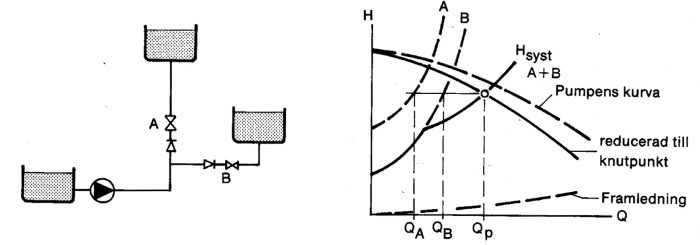
Figur 11.21 Förgrenat rörsystem med statisk uppfordringshöjd.

I det tredje exemplet reduceras först pumpkurvan till knutpunkten. Därefter adderas systemkurvorna för grenarna A och B till den resulterande systemkurvan Hsyst A+ B. Skärningspunkten mellan den reducerande pumpkurvan och den resulterande systemkurvan bestämmer pumpens driftspunkt enligt figur 11.21.

Figur 11.22 Förgrenat rörsystem med fallande framledning.

I det fjärde exemplet råder en nivåskillnad (i detta exempel en tillrinningshöjd) mellan behållaren på pumpens sugsida och knutpunkten. Systemkurvan för framledningen uppvisar därför en statisk uppfordringshöjd (Hstat <0).Metodiken är densamma som i tidigare exempel. Först reduceras pumpkurvan med framledningens kurva till knutpunkten. Därefter bestämmes systemkurvorna för grenarna A och B utgående från knutpunkten. Grenarnas resulterande kurva matchas mot pumpens reducerade kurva enligt figur 11.22. Med denna metodik kan i princip hur komplicerade rörsystem som helst med hur många knutpunkter som helst beräknas. De längst bort liggande grenarnas resulterande systemkurva i förhållande till den längst bort liggande knutpunkten bestämmes. I nästa steg behandlas nästa knutpunkt osv tills man når fram till knutpunkten närmast pumpen.

Föränderliga systemkurvor

Under vissa speciella förhållanden kommer systemkurvorna att förändras med driftsituationen. Nedan ges några exempel på sådana situationer.

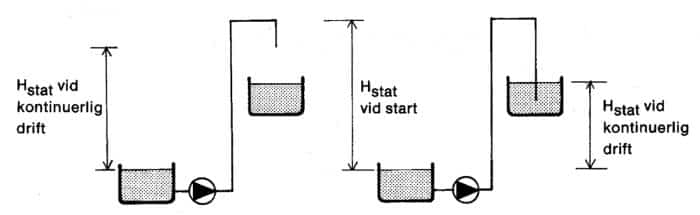
Figur 11.23 Statisk uppfordringshöjd vid start och vid kontinuerlig drift.

Vid start är ledningen fylld med luft. Pumpen måste lyfta vätskan till ledningens högsta punkt. Då ledningen är helt vätskefylld reduceras den statiska uppfordringshöjden. Om pumpens uppfordringshöjd i dämda punkten ej överstiger Hstat vid start kommer pumpningen inte igång.

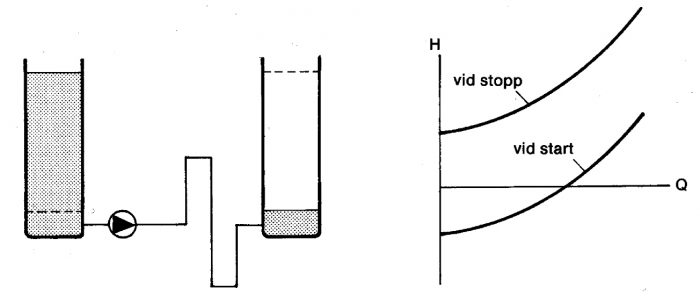
Figur 11.24 Systemkurva med varierande statisk uppfordringshöjd.

För anläggningen i figur 3.24 kommer statiska uppfordringshöjden att variera då nivåskillnaden mellan vätskeytorna i behållarna varierar. Likartade förändringar av systemkurvan erhålles vid slutna behållare i vilka trycket är beroende av driftsituationen. Även systemkurvans förlustdel kan förändras med driftsituationen. Exempel på detta är inverkan av Reynolds tal vid varierande strömningshastigheter, icke-newtonska vätskors uppträdande, sedimentering vid transport av fasta partiklar uppslammade i vätska, kemiska processer i vätskan under transporten etc.

En avsiktlig förändrig av systemkurvans förlustdel arrangeras vid strypreglering. Då rörledningen försmutsas eller rostar ökar strömningsmotståndet. Det är inte ovanligt att förlusthöjden av denna anledning fördubblas efter längre tids drift.